Can Matrix Determinant Be Negative
Yes the determinant of a matrix can be a negative numberBy the definition of determinant the determinant of a matrix is any real number. 415 60 votes Yes the determinant of a matrix can be a negative number.

Linear Algebra Ch 2 Determinants 8 Of 48 Example Of Rule 2 The Negative Of A Determinant 3x3 Youtube
Yes the determinant of a matrix can be a negative numberBy the definition of determinant the determinant of a matrix is any real number.
. More on this can be. Singular matrices act as a boundary between matrices whose. The determinant can be a negative number.
That is because the determinant of a matrix product of square matrices equals the product of their determinants. It cannot be negative since the covariance matrix is positively not necessary strictly defined. By the definition of determinant the determinant of a matrix is any real number.
The determinant of a matrix is not always positive. This is applicable to both upper-triangular and lower-triangular matrices. Can determinant of covariance matrix be negative.
The determinant of a matrix is the scalar value or number calculated using a square matrix. Thus it includes both. Thus it includes both.
3 8 4 6. Thus it includes both positive and negative. 485 15 votes Yes the determinant of a matrix can be a negative number.
It cannot be negative since the covariance matrix is positively not. The determinant only exists for square matrices 22 33. The determinant is a special number that can be calculated from a matrix.
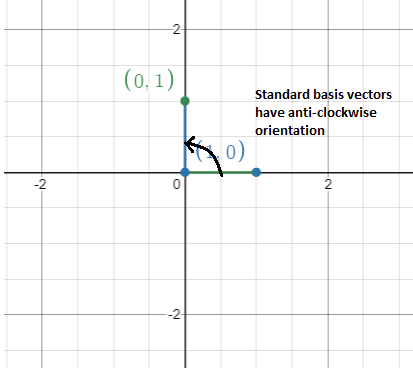
This is whats meant by space reversed its orientation. The square matrix could be 22 33 44 or any type such as n n where the number of column. Including negative determinants we get the full.
A 2X2 matrix represents a 2-dimensional space as we only have x and y-axis values as we move up to the 33 matrix we have Z-axis also which takes us to the 3rd dimension. Thus it includes both. Thus it includes both positive and negative numbers along with fractions.
What does a determinant. By the definition of determinant the determinant of a matrix is any real number. Definition of determinant.
The determinant of a matrix is not always positive. By the definition of determinant the determinant of a matrix is any real number. The determinant of a triangular matrix can be found by calculating the product of all its diagonal entries.
415 60 votes. Yes the determinant of a matrix can be a negative number. Thus it includes both.
This one has 2. The matrix has to be square same number of rows and columns like this one. The determinant of a matrix is any real number.
It is not associated with absolute value at all except that they both use vertical lines. Det A B det A det B. 485 15 votes.
Can determinant of covariance matrix be negative. Is a matrix singular if the determinant is negative. Suppose a matrix P has a.
Thats why the determinant of the matrix is not 2 but -2.

What Does A Negative Determinant Mean All Things Statistics
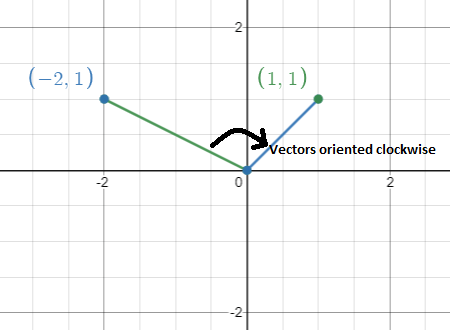
What Does A Negative Determinant Mean All Things Statistics

Linear Algebra Ch 2 Determinants 8 Of 48 Example Of Rule 2 The Negative Of A Determinant 3x3 Youtube

Chapter 3 Determinants 3 1 The Determinant Of A Matrix Ppt Download
0 Response to "Can Matrix Determinant Be Negative"
Post a Comment